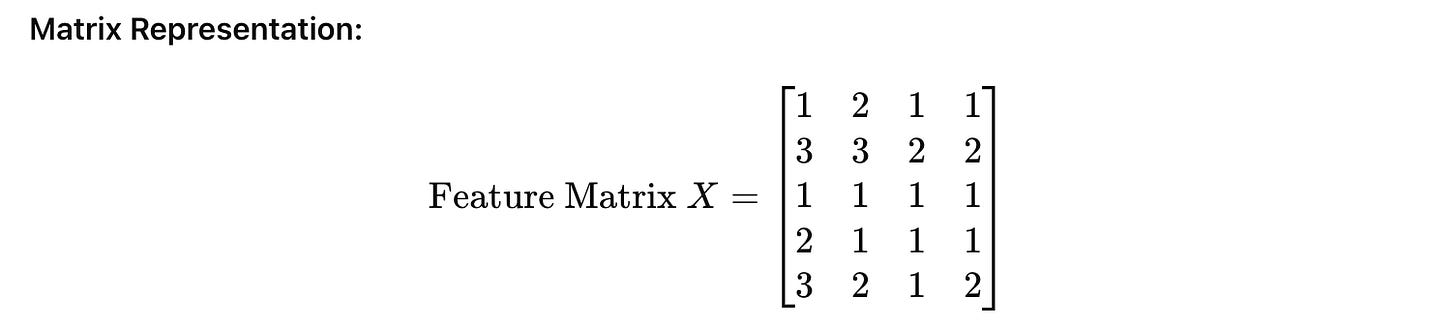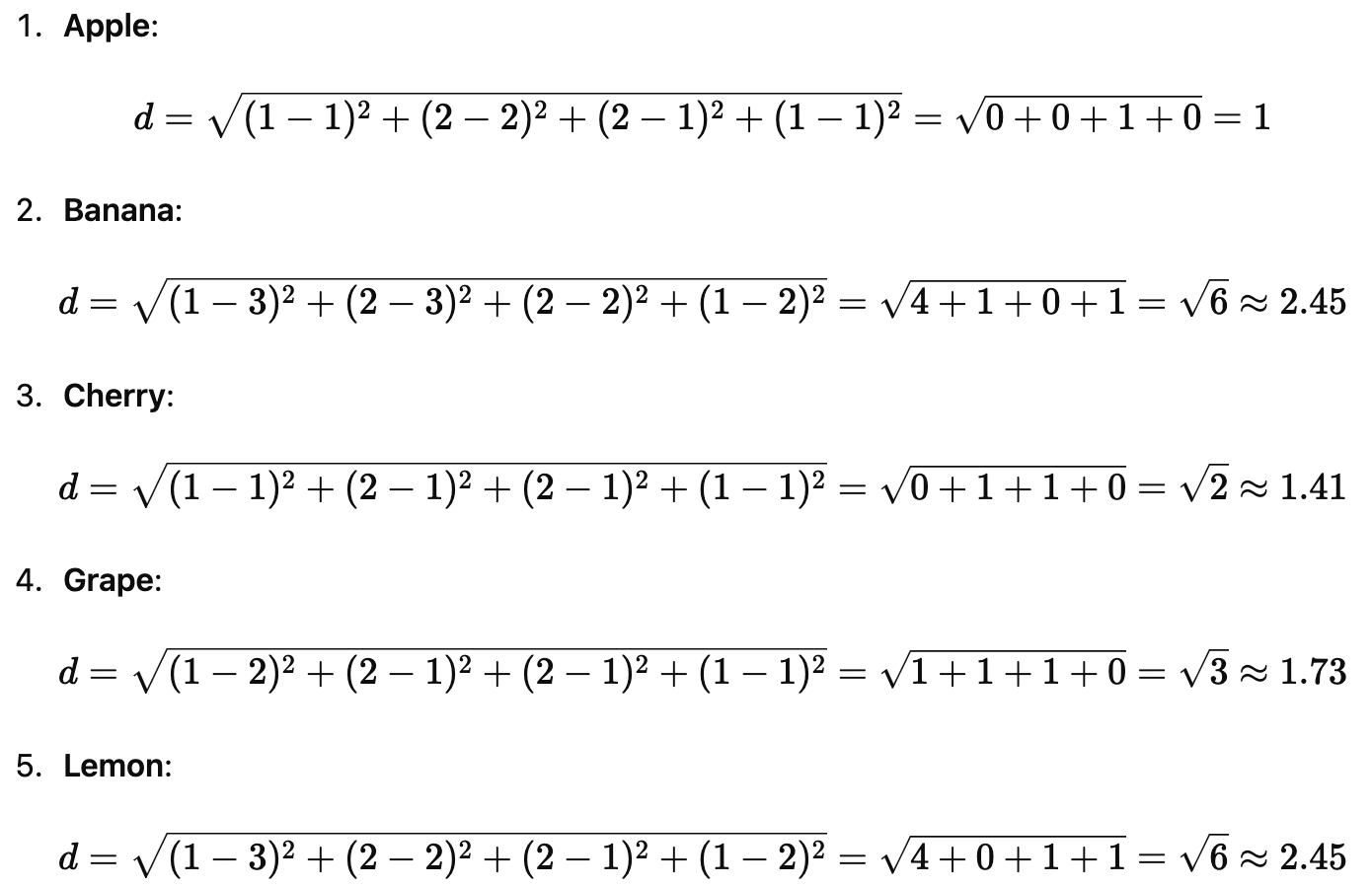An intro to artificial intelligence for newbies
For those intimidated by it, don't be(it legit all starts with a linear regression).
"It's AI for the investor, machine learning for the CEO, and a linear regression for the engineers."
I often use the quote above. Truth be told, different stakeholders perceive the complexity and terminology of AI quite differently. While investors often want to hear the buzzword "AI" to generate excitement, we engineers, who are working hands-on, may see the problem solved with something as fundamental as linear regression. The technology (chips, data centers) driving AI is impressive, but the basic math behind it, in its essence, is relatively simple. Sadly, many fail to understand how AI functions effectively and where it falls short, and there are countless instances where the perceived potential of the technology misleads people. That will be a discussion for another article. For now, let’s focus on the basics of AI here.
Even though linear regression is one of the simplest forms of machine learning used in AI, it does include many more advanced models that can handle complex patterns, non-linear relationships, and tasks beyond prediction, such as image recognition, natural language processing, and decision-making. So, while linear regression is part of the AI toolbox, AI’s core involves a broader and more complex set of algorithms.
That being said, if you are hearing about AI everywhere, but are a tad clueless as to what it is and how it works and want a basic intro, this 2-part post is for you! I have included an example for us to build our AI model right here (see below).
First, let’s define artificial intelligence.
At its core, AI is a collection of tools and techniques (mathematics, statistics, cognitive science, and computing) used to analyze data, identify patterns in the data, and use it to make predictions or decisions, without explicit programming for every scenario, simulating human learning and understanding. AI uses algorithms to learn from data, to create models that can make predictions or decisions. For instance, we as humans can predict when a person we know might get upset or be happy, based on our prior interactions with them. This is part of human cognition. AI seeks to simulate that (make predictions based on data).
Machine learning (ML) is the subset of AI that focuses on training these algorithms to find patterns in data. As AI processes more data, it improves its ability to recognize patterns and make accurate predictions.
During a training phase, the AI is fed with data, and it uses this data to build or train a model, which is essentially a set of mathematical rules or formulas. The model adjusts itself based on the data it has seen, trying to minimize errors. Once trained, the AI model can make predictions or decisions based on new, unseen data, usually called test data. For example, a trained AI model that recognizes handwritten digits can take a new handwritten number and predict what digit it represents. AI systems continue to learn and improve by analyzing more data or getting feedback. For example, if the AI makes a mistake, that mistake can be used as additional data to refine the model, making it more accurate over time. Neat, huh?
AI excels at detecting patterns, especially those that may not be immediately obvious to human observers, particularly in settings like understaffed care facilities. It can analyze large amounts of patient data—such as vital signs, lab results, and biomarkers—to identify patterns and trends.

Some AI tools use deep learning, a subset of machine learning that involves artificial neural networks with multiple layers ("deep" networks). These networks are inspired by the human brain and learn to recognize complex patterns by processing data through interconnected layers, each layer capturing more abstract features.
To understand AI better, let's explore some basic concepts using concrete examples.
Part 1: Single-Variable Linear Regression
Example: Predicting Housing Prices
Linear regression is a fundamental statistical technique that helps us understand the relationship between two variables. For example, let’s say we want to predict the price of a house based solely on its size (square footage).
Data Points: We collect data on several houses, including their size (square footage) and price. The size is then the feature being used to predict the price.
Model: We plot the data points on a graph where the x-axis represents the size of the house and the y-axis represents the price. Linear regression helps us find a line (called the "best-fit line") that represents the relationship between size and price.
Different Fits:
Underfitting: If the line does not capture the trend well (too simple), it’s called "underfitting." This happens when the model is too simplistic to capture the nuances of the data.
Overfitting: If the line tries to pass through every data point, it’s called "overfitting." This happens when the model is too complex and captures noise rather than the actual trend.
Good Fit: A well-fitted line balances simplicity and accuracy, capturing the main trend without being overly complex.
By fitting this line, we can predict the price of a house given its size. This fit is called our model.
Part 2: Multivariate Linear Regression
In real life, the price of a house is influenced by many factors, not just its size. For instance, location and finishes (quality of materials and design) also play significant roles.
Example: Predicting Housing Prices with Multiple Factors
Data Points: Now, we collect data on houses, including three variables or features:
Square footage: The size of the house.
Location: A score representing the desirability of the neighborhood.
Finishes: A score representing the quality of the house's finishes.
Model: Multivariate linear regression helps us find the best-fit line (actually, a plane in a multi-dimensional space) that represents the relationship between these three variables and the house price.
Predicting Prices: Using this model, we can predict house prices based on a combination of square footage, location, and finishes.
An AI algorithm would process this data and learn how each variable (size, location, finishes) contributes to the overall price of the house. Instead of a simple straight line like in single-variable linear regression, the AI finds a "best-fit plane" (or hyperplane in higher dimensions) that best represents the relationship between these variables and house prices. The AI adjusts the weights (coefficients) for each factor through training.
It would now look something like this:
The result is a multivariate linear regression model where each factor is assigned a weight. For example, the model might find that square footage has a large impact, but finishes have a smaller influence, while location has the most significant effect.
Once trained, this model can be used to predict house prices for new data.
Fun fact: Kaggle has a competition for folks to predict housing prices. It’s just for fun, but thousands of people attempt to find the best algorithm!
Step-by-Step: An AI Model for Fruit Classification
Let’s build a model to teach a computer to recognize fruits. To do this we provide labeled images of apples, cherries, grapes, lemons, and bananas. The AI analyzes these images to learn identifying features, like color and shape. When shown a new image, it uses the model to predict the fruit type, improving as it receives more data and feedback. We will build a model to do this below.
Step 1: Define the Features
We'll start by defining the features that describe each fruit:
Color: Encoded as numerical values (e.g., Red = 1, Green = 2, Yellow = 3).
Size: Encoded as numerical values (e.g., Small = 1, Medium = 2, Large = 3).
Shape: Encoded as numerical values (e.g., Round = 1, Oval = 2).
Texture: Encoded as numerical values (e.g., Smooth = 1, Rough = 2).
Step 2: Construct the Feature Matrix
Now, we'll create a matrix where each row represents a fruit, and each column represents a feature.
Let's assume we have 5 fruits:
Each row in this matrix corresponds to a fruit (Apple, Banana, etc.), and each column represents a feature (Color, Size, Shape, Texture).
Step 3: Define the Target Vector
We also need a target vector that represents the type of fruit. We'll encode the fruit types as follows:
Apple = 0
Banana = 1
Cherry = 2
Grape = 3
Lemon = 4
Step 4: Choose a Classification Algorithm
For simplicity, let's use the k-Nearest Neighbors (k-NN) algorithm. The k-NN algorithm classifies a data point based on the majority class of its 'k' nearest neighbors in the feature space.
Calculate the Distance: To classify a new fruit, we compute the distance between the new fruit and all fruits in our matrix. We'll use the Euclidean distance:
where x1,y1, z1 and w1 are the feature values of a new fruit and x2,y2,z2,w2 are the feature values of an existing fruit in our dataset.
Choose the Nearest Neighbors: Select the 'k' fruits with the smallest distance to the new fruit.
Determine the Fruit Type: Assign the new fruit the type that is most common among its 'k' nearest neighbors.
Step 5: Classify a New Fruit
Let's classify a new fruit with the following features:
Color: Red (1)
Size: Medium (2)
Shape: Oval (2)
Texture: Smooth (1)
New fruit vector:
New fruit=[1221]
We'll calculate the distance from this new fruit to each fruit in our matrix:
Step 6: Determine the Nearest Neighbors
Let's choose k=3 (the 3 closest neighbors).
The three smallest distances are:
Apple: 1
Cherry: 1.41
Grape: 1.73
Step 7: Predict the Fruit Type
Among the 3 nearest neighbors:
Apple (0): 1
Cherry (2): 1
Grape (3): 1
Since each type appears once, we might either increase kkk or decide by proximity. The new fruit is closest to Apple with a distance of 1.
Result: The model predicts the new fruit is likely an Apple.
Furthermore, one can use SHAP values (Shapley Additive Explanations) to determine which feature drives the model most. SHAP values are a method used to explain the output of complex machine learning models by measuring the contribution of each feature to a particular prediction.
Matrix Multiplication is the BackBone of AI
Matrix multiplication is at the heart of how AI systems, like ChatGPT, process data, learn patterns, and generate responses. Every time you interact with an AI, the system transforms your input (like text) into numbers. These numbers are stored in matrices, which are large grids of values. The AI multiplies your input matrix with other matrices, the weight matrices (representing what the AI has learned) to understand and process your request. This multiplication allows AI systems to compute new representations of the data as it moves through the network.
At the core of matrix multiplication is something called the dot product, which measures how closely input data (like words in a sentence) relates to what the AI has learned (its "weights"). Each value in the result is a combination of many smaller multiplications, repeated millions of times in one task, enabling the AI to analyze and understand complex information.
During training, the AI adjusts its weights to improve accuracy. The AI calculates the difference between its prediction and the correct answer (the error), and then uses this error to adjust its weights. This process, called backpropagation, involves multiplying the error by gradients of the weights (also calculated through matrix multiplication) to fine-tune the system and make better predictions in the future.
For instance, in a neural network, each layer transforms the data using matrix multiplication. The AI "learns" by adjusting these matrices based on errors it makes, improving its predictions over time. When the AI processes data, it does millions of these matrix multiplications, which makes it capable of handling complex tasks.
If AI is just complex math (and lots of linear algebra), why is it taking off now?: AI's Dependence on Silicon Technologies
AI relies heavily on matrix multiplication, especially in models like GPT-3, where vast amounts of data and parameters are processed using large matrices. For example, in GPT-3, a typical operation involves multiplying matrices as large as (2048 x 12288) and (12288 x 49152), with each result being the dot product of vectors requiring thousands of multiplications and additions. The challenge in AI isn't just the math; it's doing these massive computations efficiently.
As models get larger (think billions of parameters), the process becomes more tedious and complex. This is why hardware optimizations like quantization (reducing number precision) and parallel processing (doing many multiplications at once) are essential for AI systems to work quickly and efficiently (imagine waiting hours per prompts).
Matrix multiplication, especially at this scale, is computationally demanding. While AI concepts have been around for decades, the ability to execute these tasks efficiently was limited by the available hardware. Only recently, advances in silicon integrated technologies have provided the necessary computing power to handle these calculations at scale. With the advent of specialized AI hardware, these computations can now be executed in parallel, vastly reducing the time required to perform each operation.
Quantization has been a game-changer in enhancing the efficiency too. By reducing the precision of the numbers used in computations—from 32 bits to 16 bits, and further to 8 bits—networks can run faster and use less power. Even companies like Nvidia attribute much of their hardware advancements—up to a 16x improvement in single-chip performance over the last decade—largely to the adoption of lower precision number formats. For comparison, the shift in silicon manufacturing processes from 28nm to 5nm technology has only yielded a 2.5x improvement in efficiency (this SemiAnalysis piece linked is well worth the read).
These matrix multiplications aren’t carried out sequentially—modern hardware means we can do thousands or millions of operations in parallel. In other words, that is why it can generate responses in real-time, even though the underlying operations are computationally intensive.
Power and Efficiency Challenges in AI
Even though computer performance has greatly improved, the biggest challenge to making machine learning chips even better is how much power they use. For example, chips like Nvidia’s H100 can theoretically handle 2,000 trillion operations per second (it has about 2000 teraflops), but in reality, power limitations stop them from reaching that full potential. Each Nvidia H100 GPU consumes about 700 watts of power, which restricts its ability to fully reach its theoretical performance in practice.
As AI models keep growing and require more calculations, the efficiency of how much work the chip can do per unit of energy becomes really important. Thus, efficiency—measured in floating point operations per joule of energy—is a critical focus for AI hardware.
Types of AI
AI can be categorized in different ways (functionality, capability, etc.) , but overall it is key to distinguish between 2 main types: predictive and generative AI.
Predictive AI: This type focuses on forecasting outcomes or events based on data. Predictive AI is criticized in the book AI Snake Oil for being overhyped and failing to meet expectations in many fields. Predictive AI tools are used in areas like healthcare, criminal justice, and civil war prediction, but often do not perform better than traditional statistical methods, and many claims about their effectiveness are not reproducible.
Generative AI: This refers to AI systems that can generate new content, such as text, images, code, or audio. Large language models like ChatGPT fall into this category, and they have gained significant attention for their ability to produce coherent and creative outputs.
BONUS: How well does a ML model work?
Once a model is built, we can test it against new data. We can then grade how well our model predicts outcomes. We will get into the details of this at another time, but for now, these are the main metrics:
Accuracy: The proportion of correctly predicted instances (both true positives and true negatives) out of the total instances.
Precision: The proportion of true positive predictions out of all positive predictions made by the model.
Recall (Sensitivity or True Positive Rate): The proportion of true positive predictions out of all actual positive instances.
F1 Score: The harmonic mean of precision and recall, balancing the two.
Specificity (True Negative Rate): The proportion of true negative predictions out of all actual negative instances.
Type I Error (False Positive Rate): The rate at which the model incorrectly predicts a positive outcome when the actual outcome is negative.
Type II Error (False Negative Rate): The rate at which the model incorrectly predicts a negative outcome when the actual outcome is positive.
Area Under the Curve (AUC) - Receiver Operating Characteristic (ROC) Curve: AUC represents the area under the ROC curve, which plots the true positive rate (sensitivity) against the false positive rate (1 - specificity) at various threshold settings.
Confusion Matrix: A table used to describe the performance of a classification model by displaying the actual versus predicted classifications.
Logarithmic Loss (Log Loss): Measures the performance of a classification model by penalizing incorrect classifications. Log loss increases as the predicted probability diverges from the actual label.
Mean Squared Error (MSE): Commonly used to measure the average squared difference between predicted and actual values in regression tasks.